Spectral and Algebraic Graph Theory Ch15 - Tutte's Theorem - How to draw a graph

本期专栏为 “谱图理论” 系列的第15期，将介绍耶鲁大学教授、两届哥德尔奖得主 Daniel A. Spielman 所著图书 《Spectral and Algebraic Graph Theory》 电子版链接 第十五章 Tutte’s Theorem: How to draw a graph 中的内容。

本期作者 | 丁海鹏，中国人民大学高瓴人工智能学院

15.0 概要

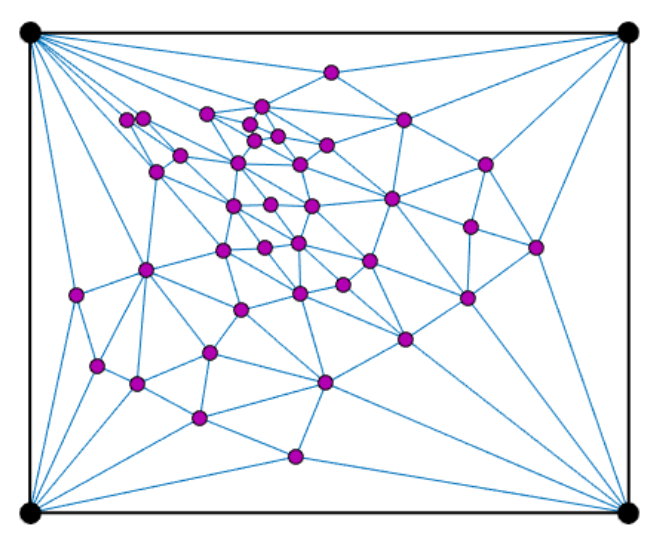
塔特定理介绍了如何利用弹簧网络嵌入来获得一个\(3\)-连通平面图的平面嵌入。当我们选定一个平面图的面，并将该面相关联的结点都固定在一个平面上，弹簧网络的性质告诉我们所有未被固定的点都处于它所相邻节点的重心位置（边原长为0，且所有边具有相同的弹性系数），即其邻居节点的位置均值。而塔特证明了，此方法对于一个\(3\)-连通图，将产生一个正确的平面嵌入（示例如下图）。

15.1 \(3\)-连通图，平面图

令连通图 \(G=(V,E)\)，那么：

若 \(G\) 是一张 \(k\)-连通 图，那么对于图 \(G\), 移除图 \(G\) 中的任意 \(k-1\) 个节点都不会使图变得不连通。

\(3\)-连通图是一个在图论中被广泛研究的图种，其有相当多优秀的图论性质。在本章中，我们更加关心此类图的代数性质。一些图论结论将被介绍并使用，但不作证明。

若 \(G\) 是一张平面图，那么对于图 \(G\), 存在映射 \(z:V\rightarrow\mathbb{R}^2\), 使得对于任意 \((a,b)\in E\), \(z(a)\) 与 \(z(b)\) 在平面 \(\mathbb{R}^2\) 上可以曲线相连，且曲线互不相交，也不经过除了 \(z(a)\) 与 \(z(b)\) 外的其他节点。

一言以蔽之，若一张图为平面图，那么它一定可以画在一张纸（谓之为平面）上，而所有的边互不相交，边也不会经过除了始末点以外的节点。而画在纸上的一种方法，便可以理解为平面嵌入。平面图定义下有较多的子概念，我们将逐一介绍。

直观地看，在一个平面嵌入中，我们将一个平面分割为很多部分。每一个部分被称为面。同样地，整张图最外侧无限大的平面，也是一个面。

此处我们将结合\(k\)-连通的相关知识，介绍一些平面图与面的相关性质。

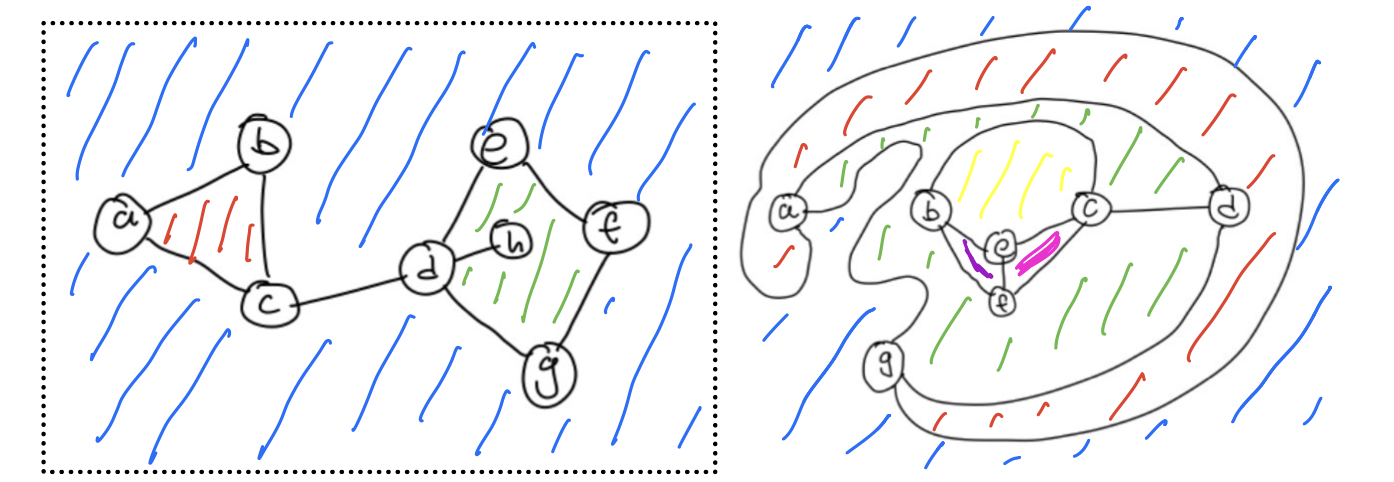
如上图所示，这两张图都是 \(1\)-连通的。左子图共有三个面，其中边 \((d,h)\) 在绿色面中出现了两次。而右图有着较为复杂的划分，且存在重边 \((a,g).\)

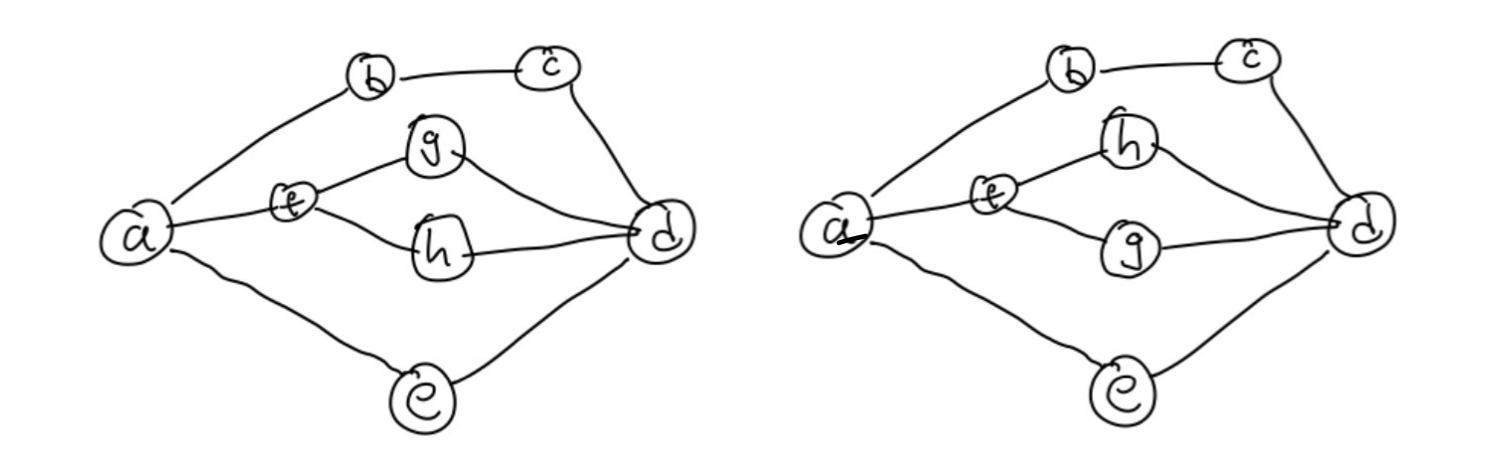
如上图所示，这两张图都是 \(2\)-连通的，而且很显然，这两张图是同构的，但是是不同的平面嵌入。我们调换了点 \(g,h\) 的位置，但两张图构成面的元素（节点/边）集合发生了改变。

我们在这里仅研究\(3\)-连通的无重边自环图。一个优秀的性质是，对于一个\(3\)-连通图，其任何形式的平面嵌入，都不会改变构成面的元素集合。

Claim 15.1.1 令 \(G=(V,E)\) 为一\(3\)-连通的平面图，而 \(F\) 为图 \(G\) 对应的面集合，其中每个面对应了原图中的一个环。那么，没有节点在同一个面中出现两次，没有边在同一个面中出现两次，且每条边仅出现在两个面中。

如上图所示，我们可以通过形如 \(abf,fgh\) 的方式来描述一个面。对于构成最外侧无限大面的边集合，我们称之为边界，即 \(abcde\).

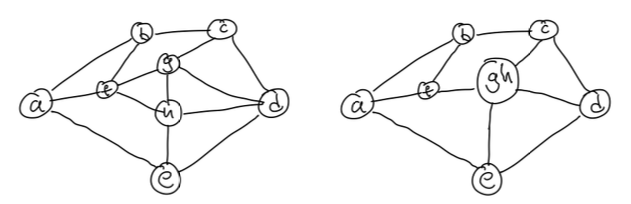
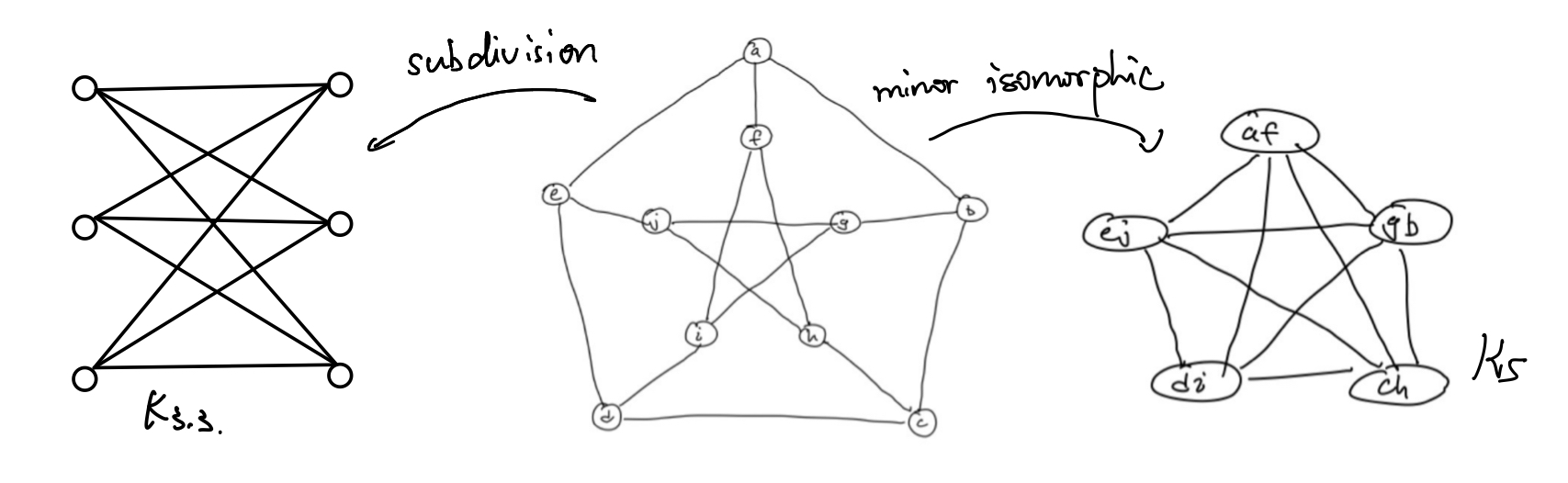
此处介绍边收缩运算，其直观描述可参考右图（对左图边 \((g,h)\) 收缩）。边收缩运算会删除原图与该边相关的两个节点，加入一个新的节点并向原两个节点的邻居连边。边收缩运算将保持平面图的平面性质，与\(3\)-连通图的\(3\)-连通性。如果图 \(H\) 是图 \(G\) 进行若干边收缩后的子图，那么我们称 \(H\) 是 \(G\) 的一个图子式。

Theorem 15.1.2 Wagner’s Theorem 图 \(G\) 是平面图，当且仅当图 \(G\) 不存在一个与 \(K_5, K_{3,3}\) 同构的图子式。其中，\(K_5\) 是一张由五个点组成的完全图，而 \(K_{3,3}\) 是一张两侧各有三个点的完全二分图。

Remark

该定理的应用较为困难，但很明显，上图可通过边收缩获得一个图 \(K_5\)。需要注意的是，删除节点，删除边是取子图所允许的操作，在上图的例子中并没有体现。

本书中作者称该定理为 Kuratowski’s theorem. 事实上，定理 Kura. 的描述是：图 \(G\) 可平面图的充要条件为不存在与 \(K_5,K_{3,3}\) 同构的同胚子图。而同胚通过在一条边中插入一个2度节点，或删除一个2度节点并连接与其相关联的边所定义。读者有兴趣的话，可以构造上图有一与 \(K_{3,3}\) 同构的同胚子图，此处不再赘述。

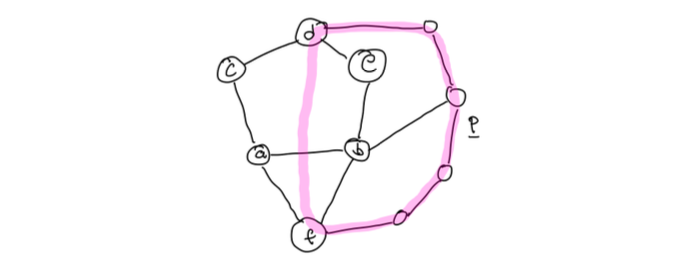
Lemma 15.1.3 令 \((a,b)\) 为一\(3\)-连通图中的边，而 \(S_1,S_2\) 为包含该边的两个面。令 \(P\) 为图 \(G\) 中一起点为 \(S_1-\{a,b\}\)，终点为 \(S_2-\{a,b\}\) 的路径，且不与 \(a\) 或 \(b\) 相交。那么，图 \(G\) 中任意从 \(a\) 到 \(b\) 的路径必与路径\(P\)相交，或直接经过边 \((a,b)\).

Proof of Lemma 15.1.3

设\(s_1,s_2\)为路径 \(P\) 的始末点（上图的点\(d,f\)），那么对于图 \(G\) 的任意一个平面嵌入，我们一定可以找到一条曲线，只经过面 \(S_1,S_2\) 与边 \((a,b)\). 因此，该曲线在平面上连同路径 \(P\) 形成一个环，分隔开点 \(a,b\)，且仅有曲线 \(s_1,s_2\) 与图中的边交叉。那么，很显然，对于任意从 \(a\) 到 \(b\) 的路径，一定会与该环相交，要么与路径 \(P\) 相交，要么经过边 \((a,b)\).

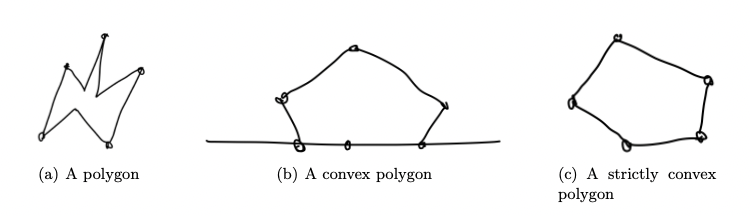
15.2 严格凸多边形

相信凸多边形对大家来说是一个非常熟悉的概念了。对于一个平面区域，若对于任意区域内的两个点，其连线段也完全在该区域内，那么这个区域就是凸的。而凸多边形，需要在此概念上加上该区域的边界由有限条线段构成。严格凸多边形则要求边界线段构成的夹角均小于\(\pi\).

换言之，一个严格凸多边形要求对于任一边界线段，整个多边形在其延长成的直线的一侧。除了该线段的两个端点，没有其他的端点在这条直线上。

Definition 15.2.1 令 \(G=(V,E)\) 为一\(3\)-连通平面图。我们称 \(z:V\rightarrow\mathbb{R}\) 是一个塔特嵌入，若：

1. 选取一个面 \(F\), \(z\) 将 \(F\) 所有的节点映射为一个严格凸多边形的顶点。该面的每一条边顺次连接顶点并形成一个严格凸多边形。
2. 每个不在 \(F\) 中的节点，根据弹簧网络的性质，每个节点都在其邻居节点的重心位置。

证明塔特定理，实际上就是证明塔特嵌入是一个平面嵌入。我们将证明一个图 \(G\) 的塔特嵌入，将其所有面都映射成了一个严格凸多边形。我们将不使用每个节点都在其邻居节点位置均值这一特性，而只需要每个节点都在其邻居形成的凸包内。这将允许弹簧网络中边具有不同的弹性系数。

Theorem 15.2.2 令 \(G=(V,E)\) 为一\(3\)-连通平面图，\(z\) 是 \(G\) 的一个塔特嵌入。如果我们将原图中所有的边仍以线段的形式连接映射后对应的端点，这将形成一个图 \(G\) 的平面画法。

如果图 \(G\) 不是 \(3\)-连通的，那么塔特嵌入可能会退化。一件很直观的事情是，如果删除 \(a,b\) 将破坏图的连通性，那么存在一个破坏后的连通块，其所有点在 \(a,b\) 构成的线段上。

我们将通过证伪所有退化情况的存在，以证明该定理。

15.3 可能的退化

1. 我们不希望节点重合，即 \(z(a)=z(b)\)，我们将在下一节阐述该内容；
2. 我们不希望一个节点 \(a\) 的所有邻居在同一条直线上，我们将在本节阐述该内容。

从本处开始，我们将不特别阐述对于边界点的特殊情况，除非必要。

Claim 15.3.1 对于一个节点 \(a\)，和任意经过 \(a\) 的直线 \(\ell\). 若\(a\)存在某个邻居在直线 \(\ell\) 的一侧，那么一定存在另一个邻居在该直线的另一侧。

这很直观。若某点的所有邻居都在节点的一侧，那么该点会因为弹力合力不为0而被拉向受力的一侧。

Claim 15.3.2 对于边界面 \(F\), 所有不构成边界面 \(F\) 的点（即非边界点）一定严格落在 \(F\) 所构成严格凸多边形的内部。

该声明可以利用将凸多边形外的点内移会降低弹性势能来解释。从更代数的角度看，所有的节点位置将表示为其邻居节点的位置均值，可解得所有节点的位置一定是边界点位置的加权平均，则一定不落在边界外。由于图是 \(3\)-连通的，那么这个加权平均至少与三个边界点有关，则不会落在边界上。

Lemma 5.3.3 令 \(H\) 是 \(\mathbb{R}^2\) 空间下的半平面（包括分隔半平面的直线）。那么，对于图 \(G\) 关于点集合 $${a

z(a)\in H}$$ 的导出子图是连通的。

Proof of Lemma 5.3.3 我们可以将分隔半平面的直线定义为 \(Ax+By+C=0\),亦或是 \(\mathbf{t}^T\mathbf{x}=\mu\). 那么，半平面进一步定义为 \(\mathbf{t}^T\mathbf{x}\ge\mu\).

对于所有节点 \(c\)，定义\(t(c)=\mathbf{t}^Tz(c)\)，这个值反映了点到直线的距离。我们找到该值最大的点，记为点 \(b\). 显然点 \(b\) 一定在边界上。若存在点 \(t(d)=t(b)\)，那么由边界面 \(F\) 被映射为严格凸多边形，\((b,d)\) 一定存在且是一条边界，且不存在其他与 \(b,d\) 共线的节点。

对于其他任意节点 \(c\), 首先找到所有 \(t(c')=t(c)\)，且 \(c'\) 是点 \(c\) 的邻居的点。所有的 \(c'\) 与节点 \(c\) 共同构成点集 \(C\). 由于原图 \(G\) 是连通的，那么点集合 \(C\) 一定存在邻居 e, 使得 \(t(e)\ne t(c)\). 那么，一定同时存在 \(t(e_1)>t(c)\) 和 \(t(e_2)<t(c)\). 这样，对于所有\(t(c)\ne t(b)\)，我们就可以找到一条函数值 \(t(\cdot)\) 不下降的路径，使得函数值 \(t(\cdot)\) 增加。由于图是有限的，增加有限次后一定会到达点 \(b\) (或点 \(d\)，若有). 那么，从所有节点出发，都可以通过一条路径到达点 \(b\)，故该子图连通。

Lemma 15.3.4 没有任何节点和它所有的邻居都在同一条直线上。

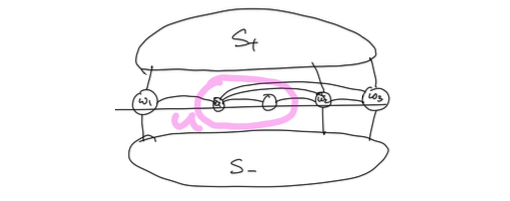
Proof of Lemma 15.3.4 反证法。假设存在节点\(a\)，它和它的所有邻居都在同一条直线上。我们进行如下构造：

1. 集合\(U\): 由 \(a\) 和它的部分邻居构成。这些邻居的所有邻居也要求全部在 \(a\) 和 \(a\) 的邻居所构成的直线上。我们称该直线为 \(\ell\)
2. 节点 \(w_1,w_2,w_3\)，是集合 \(U\) 中节点的其他邻居，也在直线\(\ell\)上，但它们有非直线\(\ell\)上节点的邻居。这样的节点至少有 \(3\) 个，否则我们可以删除所有这样的节点，使集合 \(U\) 不连通于剩下的部分，从而与原图 \(G\) 的 \(3\)-连通性矛盾。
3. 集合 \(S^+,S^-\)，表示不包括直线 \(\ell\) 上节点，由直线 \(\ell\) 分隔开两个半平面内的邻居。我们已经证明，包括直线 \(\ell\) 上节点，半平面内的节点是连通的，且所有的 \(w\) 节点均有两侧的邻居。

故，由上述示意图，由 \(S^+,S^-,U\) 为一侧，\(w_1,w_2,w_3\) 为另一侧，构成完全二分图 \(K_{3,3}\)，与原图 \(G\) 为平面图矛盾。因此假设不成立，故不存在任何节点与它所有的邻居共线。

15.4 所有的面都是凸多边形

Lemma 15.4.1 令 \((a,b)\) 图的任意非边界边，以及 \(\ell\) 为穿过 \(z(a), z(b)\) 的直线。令 \(F_0,F_1\) 为构成元素中包含边 \((a,b)\) 的两个面，\(S_0,S_1\) 为构成对应面去除点 \(a,b\) 的点集。那么，\(S_0\) 中节点的平面嵌入将落在 \(\ell\) 的一侧，\(S_1\) 的将落在另一侧，且没有任何节点落在 \(\ell\) 上。

Remark

该引理暗示了对于一个面与构成该面的一条边，构成该面的所有其他点都在该面的一侧，这恰好是严格凸多边形的定义。证明该定理，即证明了在塔特嵌入下，所有的面都被映射成了一个严格凸多边形。除此之外，任意一条边都将成为两个面的分界。

值得注意的是，该定理包含了 \(z(a)\ne z(b)\)，一种提到过的退化情况。 如果两个点嵌入重合，则可以轻松找到一条直线穿过这两个点，再穿过一个点集 \(S_0\) 中的点。

本节证明内容非常具像化，可能需要读者在纸上画一画，感受平面图与面的潜在性质。

Proof of Lemma 15.4.1

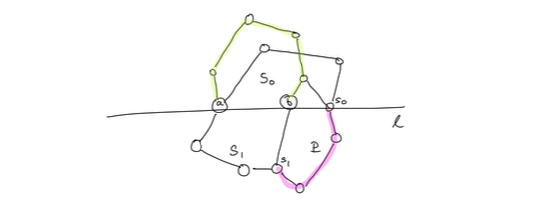
反证法。不失一般性地，我们用 上/下侧 来描述直线 \(\ell\) 的两侧，并存在 \(S_0,S_1\) 中的节点都在 \(\ell\) 下侧（或直线上）。那么我们通过 Lemma 15.3.1&15.3.4+15.3.3，了解到点 \(a,b\) 有在 \(\ell\) 下侧的邻居，且这两个邻居可以通过 \(\ell\) 严格下侧子图中的路径 \(P\) 直接到达。

同样地，\(a,b\) 也可通过一条 \(\ell\) 上侧子图中的路径直接到达，因为它们一定有上侧的邻居。但根据假设，两个构成面的点集 \(S_0,S_1\) 都在下侧，那么连通 \(a,b\) 的上侧路径不经过 \(P\)，也不经过边 \((a,b)\)，这与 Lemma 15.1.3 矛盾，故假设不成立。

上图描述了一个假设的例子。其中黄绿色路径为合法的上侧路径，两条未染色的路径为一条合法的下侧路径，和不合法的上侧路径。直线 \(\ell\) 上的点 \(s_0\) 描述了一个假设中导致上侧路径不合法的关键节点，而粉色路径则为路径 \(P\)。

Proof of Theorem 15.2.2 塔特定理

考虑一个在嵌入平面内，但不与任何节点重合，也不在任一边上的点。我们称之为平凡点。我们将要证明，对于任意一个平凡点，它一定落在且仅落在一个面内。

对于一个全图外侧的平凡点出发，它一定落在且仅落在外面 \(F\) 内。我们从任一外侧平凡点出发，画一条曲线到达任一图内部的平凡点。注意，该曲线仅能穿过边，而不穿过节点，也不能穿过两条边的交点（此处我们并没有证明两条边不能相交），这是显然可以做到的。由 Lemma 15.4.1，曲线穿过一条边将产生一次面的切换，而不会增加所属面的数量。因此，任一平凡点仅能处于一个面内。

假设存在两条边相交，那么由 Lemma 15.4.1，这两条边一定不会构成同一个面。也就是说，在这两条边交点的邻域内，一定存在某平凡点属于多个面，矛盾。

至此，我们完成了对于一个塔特嵌入，任何面都被映射成严格凸多边形，任何点都不会重合，且任何边都不会相交的证明。因此，塔特嵌入是一个平面嵌入，塔特定理证毕。